Bucket Leak How Long to Fill Continuity Equation

1. Introduction

With the rapid development of water conservancy projects, hydraulic project design and energy dissipation and anti-flooding problems have become the focus of research on discharge systems [1]. This study examines the ShiZiYa reservoir project, in which the channel in the dam site is narrow, and the angle between the axis of the drainage building and the downstream river is approximately 70°. When the water is released, it flows directly to the opposite side of the slope, thus affecting the stability of the bank slope. Therefore, choosing a suitable flip bucket is crucial to the safety downstream.

Flip buckets are one of the most common energy dissipation methods. The complex diversity of engineering topography has led to various types of flip buckets being proposed, and the energy dissipation methods include symmetrical curved surface sticking, angle narrow gap slits, special-shaped oblique nose slits, dovetail slits, and high and low slits [2,3,4,5]. Deng [6] proposed a swallowtail slit, which was a new type of pick and flow energy dissipater. Because the base plate was partially hollow and looks like a swallowtail, this system was referred to as the swallowtail slit. Although the dovetail slit is similar to the slit hybird-type flip buckets, the dovetail slit does not experience cavitations. This new flip bucket system has been installed in the first stage of the Jinping Hydropower station on the Yalong River and in the Huangdeng Hydropower station on the Lancang River, and the resulting energy dissipation and anti-shock properties were verified as ideal [7]. The swallow-shaped bar is another new type of flip bucket, and a layout including a forward swallow-shaped bar is used at the exit of the spillway tunnel in the Jinping first stage hydropower station [8,9,10]. Mao [11] used the Huangdeng hydropower station as the background for an investigation of the applicability of swallowtail bars through hydraulic model tests. The results showed that, compared to the traditional cantilever, the swallowtail cantilever could effectively increase the longitudinal distance of the water nappe, avoid scouring of the downstream slope by the drainage flow, and reduce the fluctuation in the water flow in the tailrace area. Dai [12] studied the NanYe II hydropower station in Laos, in which the spillway utilized a dovetail slit as the energy dissipation method. The results showed that a dovetail slit could effectively solve the problem of low flow and address low flow flip trajectory bucket problems. Qiu et al. [13] proposed an energy dissipation scheme of an oblique nose cantilever flow based on the narrow topography conditions of the Tihua reservoir in Yunnan province. As a result, the water flowed smoothly in the main channel, and erosion of the riverbed was reduced. Wu [14] studied the effect of a twisted nose bar on the energy dissipation of a spillway tunnel, and demonstrated that a curved nose bar with a large angle of rotation could adjust the direction of the water nappe entering the water so that it followed the downstream channel. To solve the engineering problems of the ShiZiYa reservoir, the design criterion for a curved nose bar was adopted to adjust the water nappe to the downstream riverbed.

Model tests are one of the most commonly used methods to study discharge energy dissipation; this method is mature and has accumulated a large amount of experience. The experimental results of model tests are reliable and authentic, but when the prototype is relatively complex, these tests represent a heavy workload, and are time-consuming and laborious. In recent years, with improvements in computer software, numerical simulation methods have become increasingly common, and provide the benefits of lower costs, short research periods, good repeatability, and rapid simulation of the flow field with quantitative results. In this study, FLOW-3D fluid dynamics calculation software (Flow Science, Santa Fe, NM, USA) was used to simulate the discharge characteristics of a dovetail camp energy dissipation scheme, and the finite volume method was used for numerical simulation. Spalding and Patanker [15] proposed the finite volume method, which requires a relatively small amount of calculations and is the most commonly used method in computational fluid dynamics [16]. The most commonly used free surface tracing method is the volume of fluid (VOF) method, which was proposed by Hirt and Nichols in 1982 [17]. The VOF method can effectively reduce the required calculation time. Xia [18] simulated and calculated the hydraulic characteristics of the water and gas two-phase flow of a swallowtail camp using the standard k-ε turbulence model based on the VOF free liquid surface capture method. The morphological changes during the development of a swallow-tailed camp were analyzed, and the results verified that the numerical simulation was consistent with the model test results.

Dovetail-shaped bucket is a new type of overhanging bucket, which can solve the problem of the longitudinal stretching of water nappe. In this paper, a numerical simulation model of jet water through dovetail-shaped bucket is given based on a three-dimensional computational fluid dynamics (CFD), and this model is also applied to the optimization of flood discharge scheme for practical engineering problems. It is of great significance to fully understand the flow characteristics of the shape of the bucket and solve practical engineering problems.

2. Numerical Model and Validation

2.1. Numerical Model Setup

In this study, FLOW-3D fluid calculation software was used to calculate the hydraulic characteristics of the energy dissipation of a dovetail slit. The renormalization group (RNG) model was adopted for turbulence calculation. The RNG k-ε model took the turbulence anisotropy into account, corrected the turbulent viscosity, and could make complex turbulent simulation more accuracy. The control equations included the continuity equation, momentum equation, energy equation, k equation and ε equation. The VOF model was used for free surface tracking. The VOF method defined a fluid volume function F at each unit of the computational domain, when F = 1, it meant that the unit was filled with a fluid phase; when F = 0, it meant that there was no fluid phase in the unit; when 0 < F < 1, this unit was called the gas-liquid interface. The VOF model mainly used the geometric reconstruction method to determine the position of the free surface of the liquid. It could simulate two-phase flow and multi-phase flow, and by solving the momentum equation and tracking the volume fraction of the fluid in each unit, the free surface could be obtained. The water nappe spread to the downstream channel was a transient process, and VOF method had significant advantages for transient tracking.

The size of the numerical model and the dovetail sill are shown in Figure 1.

2.2. Design of the Validation Experiments

To verify the accuracy and credibility of the numerical simulation method, a simplified experiment was carried out, the purpose of this experiment being to verify the accuracy of the numerical model simulation method in simulating the air water nappe problem with complex overhanging flows. The model was designed with the Froude similarity, and the scale was 50:1. The complete experimental model included an upstream rectangular tank, water pump, WES weir, drain tank, flip bucket segment, downstream rectangular drainage trough, measuring weir, U-shaped connection back to the sink, and underground and other components of the reservoir. The slope of spillway was 30°, and the width of the model was 25 cm. The spillway end was connected with the flip bucket segment. Figure 2 shows a schematic diagram of the experimental setup.

The central axis of the arc was equipped with eight pressure orifices that measured the pressure head. The water level measuring needle at the sharp-crested weir was used to determine the flow rate, as shown in Figure 3. The flow rate for a rectangular sharp-crested was as follows:

$Q = m_{0} b \sqrt{2 g} H^{3 / 2}$

(1)

where

m_{0}

is the discharge coefficient, b is the width of the sharp-crested weir, H is the weir head, and g indicates gravity.

In this model experiment, the height of the sharp-crested weir was P = 22.9 cm, and the width of the weir was b = 40 cm. The flow coefficient for the rectangular sharp-crested weir could be calculated with the following equations.

Bazin [19] formula:

$m_{0} = (0.405 + \frac{0.0027}{H}) {1 + 0.55 {(\frac{H}{H + P})}^{2}}$

(2)

This equation was applicable for 0.2 m < P < 1.13 m, b < 2.0 m, and 0.1 m < H < 1.24 m.

2.3. Boundary Condition Setting and Mesh Convergence Analysis

The inlet boundary condition was defined as a pressure inlet (including both static pressure and dynamic pressure) according to the water level, the downstream was a subcritical flow, which was defined as a pressure outlet, and the wall boundary condition was defined as a non-slip wall boundary condition. The specific boundary conditions are shown in Figure 4. To coincide with the experiments, the same depth was used in the model. Four flow monitoring sections were defined for the mass flow calculation. When the flow in each section did not change significantly and the area of the flow difference at each monitoring section in the calculation decreased below 10⁻³, the calculation was considered to be convergent.

The scale experiment and numerical simulation were intended to analyze the hydraulic characteristics of the launching nappe under three working conditions, as summarized in Table 1.

In order to verify the influence of grid density on discharge flow, GCI (Grid Convergence Index) convergence factor [20] was used to calculate discrete error, and then the convergence of grid was judged. When the GCI convergence factors were used for judgment, at least three mesh schemes were required, and the safety factor was taken as F_s = 1.25. Taking working condition A as an example, the calculation results for the GCI are shown in Table 2.

As shown in Table 1, the GCI decreased gradually with the mesh decerasing and was less than 5%, indicating that the discrete error is small.

2.4. Comparison of Validation Results

Figure 5 shows the flow patterns of the swallow-tailed slit under three operating conditions. Owing to the angle of both sides of the spillway and swallow-tailed slit, in the middle and lateral contraction of the water nappe were obvious, and the longitudinal diffusion was sufficient. The water crown at the top of the water nappe was also obvious, and the end was fully aerated.

A comparison between the experimental and simulated results are given in Table 3, and the result indicates that both the inner edge and the outer edge of the water nappe was in good agreements. However, the position error between the downstream water surface and the highest point of the water nappe was large. The main reason for this discrepancy was that the nappe crown of measurement error and the calculation grid size were not subtle enough in the simulation process. As a result, some thin water crowns could not be simulated, and thus the simulation values for the highest point of the water nappe were smaller than the corresponding measured values. However, considering the horizontal length of the jet flow, this meshing scheme fitted well.

To compare the simulation pressure with the measured pressure under corresponding working conditions, Figure 6 shows the surface pressure along the wall of the swallow-tailed bucket between 3.31–3.87 m under working condition A. The results show that the simulation scheme was feasible.

3. Engineering Application and Case Analysis

3.1. Introduction and Research Condition

This study was based on the ShiZiYa reservoir, and a reasonable scheme was proposed to address the main energy dissipation problems. The ShiZiYa reservoir project is located along the XingLong River, which is a first-grade tributary of the LengShui River in HanZhong city, Shanxi Province. The total capacity is 5.79 million m³, with an irrigation capacity of 4.15 million m³, thus making it a type IV small engineering project. The flood control standard of the dam is based on a 200-year flood event, while it is designed according to 30-year flood levels and the energy dissipation and anti-erosion design are based on the 20-year flood standard. The spillway energy dissipation structure consists of two sand wash bottom holes, three overflow gate holes, and a spillway. The gates are numbered from left to right as #1, #2, and #3, as shown in Figure 7.

Based on the topographical characteristics and flood discharge conditions of the ShiZiYa reservoir, the deviation angles of the left and right bank sidewalls of the spillway were determined. Thus, the point at which the water nappe plunging into the water could be adjusted to the downstream main channel as close as possible. After debugging, the left sidewall angle was taken to θ₁ = 13°, the right bank sidewall angle was taken to θ₂ = 6°, and the radius R = 10.2 m. The flow state of the nappe was controlled by changing the deflecting angle and the width of the dovetail slit. Figure 8 shows the shape of the dovetail slit, while the designed schemes are summarized in Table 4.

3.2. Establishment of the Numerical Model

The calculation region of the numerical simulation was determined based on a site investigation and CAD topographic map. Using the specific data in the measured topographic map combined with the actual topography of the upstream and downstream locations and the layout of buildings in the area and their influence on the downstream flow condition, some reasonable simplifications of the actual topography and buildings were carried out, as shown in Figure 9. This study was based on a topographic model of the ShiZiYa reservoir. Upstream of the reservoir, a grid size of 2.5 m was used, while the mesh at the downstream of the reservoir was 1.5 m. The overflow dam and the discharge area were the focus of this study, hence the mesh in this location should be finer. Therefore, this area was meshed with a grid of 0.5 m, yielding a total of grid number of approximately 7 million. The boundary conditions are shown in Figure 10.

3.3. Analysis of the Calculated Results

3.3.1. Distribution of the Water Nappe Flow of Each Scheme

Figure 11 shows the flow pattern of water nappe for 200-year flood conditions under the four schemes with energy dissipation provided by a swallowtail cantilever. Comparing schemes I with II and schemes III with IV (because deflecting angle of dovetail slit in the latter schemes was 5°), it could be concluded that the longitudinal stretching effect was more pronounced. Comparing schemes I with III and schemes II with IV, (because the central opening width, B, in the latter schemes was equal to 8 m) the water flow rate increased, and the flow rate through slit on both sides decreased, which resulted in a decreasing length of the flip shot for both the nearest and farthest distances. It can be seen in Figure 11 that because the water nappe could not deflect in the air, the furthest impact position was closer to the concave bank slope, which could cause greater erosion of the bank slope.

The flowrate in this project were mainly moderate or small discharge. For further calculation of the small discharge, scheme II was used for the modeling combined with the specific engineering conditions. The flow rate was adjusted through operation of different gate openings; the specific working conditions are summarized in Table 5.

Figure 12 shows the flow pattern and location of the water nappe entry point under three working conditions for the 30-year flood standard, 20-year flood standard, and 5-year flood standard. In the case of the 30-year flood standard, because the flow discharge was large, the longitudinal extension of the water nappe was significant and continuous. In the case of the 20-year flood standard, owing to a 20% opening of the three-hole gate, the flow discharge was reduced and the water nappe was thinner. When water flowed through the slit, the stretching of this water nappe was relatively small because the deflecting angle was −5°. As a result of the compression effect of the large angle of the anti-arc segment and the angle of the sidewall, the two water streams were forced toward the central axis, and entered the downstream channel after colliding in the air. In the case of the 5-year flood standard, the flow rate was very small, the #2 surface hole was closed, and the #1 and #3 surface holes were opened to 20%.

The anti-arc notch did not play a role in this case, and the water flowed through both sides and entered the main downstream channel after collision in the air due to the extrusion of the sidewall. Owing to the friction and mixing of the water, the energy of the water flow was effectively eliminated, and the erosion of the riverbed was alleviated.

3.3.2. Distribution of the Bottom Velocity under Different Working Conditions

The velocity at the wall of the spillway and the riverbed are shown in Figure 13. The velocity at the impact point of the water nappe with the downstream riverbed was relatively large because the flow was large. The maximum velocity was approximately 32 m/s, with the main stream located in the main river location. Under working condition 3, due to the decreased flow rate, the water flow at the slit was not squeezed by the flow from both sides, but was affected by the jet angle of the slit. The water nappe in the middle thus overhung to the downstream, and had a large transverse diffusion. It can be seen in Figure 13 that the flow velocity near the bulge hill on the right bank was relatively large, which was a result of the transverse diffusion of the water nappe in the middle. The elevation of the impact point at this location was relatively low, however, less than 687 m. The flow rate was lowest under working condition 4, which was caused by the collision of two water nappes in the air with a high energy cost; the flow velocity near the bottom of the riverbed was approximately 26 m/s.

3.3.3. Distribution of the Bottom Pressure under Different Working Conditions

Figure 14 shows the pressure distribution on the wall surface of the spillway and the bottom the riverbed under various working conditions. All of the pressures of the wall surface were given for working conditions 2 and 3. The pressure on surface hole wall #2 was less than that on #1 and #3. The pressure on surface hole wall #1 and #3 were given under working condition 4, because the #2 surface hole was closed, only #1 and #3 were opening. The downward flow on both sides did not have the constraint of the #2 surface hole, but were influenced by the angle of sidewall, and the flow in the reverse arc was more disordered than under working conditions 2 and 3, causing the pressure distribution to fluctuate.

Figure 15 shows the simulation results for the pressure along the wall surface of the number 1, number 2, and number 3 spillways at locations of 0–045.75 m to 0–010 m from the dam. It can be seen that the pressure distribution at the spillway surface and bed bottom is in line with the actual results. The pressure head of the arc under working conditions 3 and 4 was significantly smaller than that under working condition 2, because the angles of both sidewalls of the spillway were different, and the extrusion effect and impact effect on the water flow were thus also different.

3.3.4. Construction and Pitch of the Water Nappe

Figure 16 shows the trajectories of the inner and outer edges of the water nappe under three working conditions: 30-year flood conditions, 20-year flood conditions, and 5-year flood conditions. These different working conditions yielded different throw distances, as summarized in Table 6.

The longitudinal stretching of the water nappe along the river was suitable under working conditions 2 and 3. The longitudinal stretching lengths were 30.5, 29.3, and 20.6 m under working conditions 2, 3, and 4, respectively. Under working condition 4, two water streams did not pass through the anti-arc notch, and enter the downstream channel after collision in the air. As a result, there was no obvious longitudinal stretching. It could be seen that the operation mode of the gate had a significant influence on the shape of the water nappe. With increasing discharge flow, the longitudinal extension of the water nappe became fully stretched, and the outer edge of the water nappe was closer to the bank slope. Thus, it was necessary to protect a certain range of the bank slope. When the discharge flow was small, although the water nappe failed to stretch along the longitudinal direction, however the inner edge distance was far, and the entry of the water nappe occurred in the main channel, which could meet the flood discharge requirements. Thus, it can be concluded that the water nappe could meet the safety discharge requirements for the ShiZiYa reservoir.

4. Summary

In this study, the FLOW-3D computational fluids software was combined with experiments to simulate overflow over a flip bucket with dovetail slits under four working conditions. The following conclusions were drawn:

Using the check flood level of 200-year flood conditions as the standard, after debugging, the angles of both sidewalls were set to θ₁ = 13° and θ₂ = 6°. Based on this, the width of width B and the deflecting angle of dovetail slit θ₃ were selected as variables. Four types of solutions were presented: B = 6 m and 8 m, and θ₃ = 0° and −5°, and the water tongue hydraulic characteristics were analyzed. The results showed that the dovetail slit could effectively stretch the longitudinal length of the water nappe. As B increased, the flow rate increased, and the inner and outer edges of the water nappe and the throw distance decreased. When the opening width was smaller, the position of the water nappe entry was effectively distributed along a straight line. When the opening width increased, the position of the water nappe entry exhibited a curved distribution, and the direction of bending was opposite that of the river channel.
This study was based on the model of scheme II, and it analyzed the 30-year, 20-year, and 5-year flood design standard conditions under three different working conditions of the characteristics of the water nappe. The results showed that different working conditions resulted in different water flow patterns, but they all could be attributed to the main river channel. The differences arose mainly due to the different operation of the gate opening, which contributed to the large difference in the pattern of the water nappe. There was a slight difference between working condition 1 and working condition 2. However, in working condition 3, three surface holes were partially opened by 20%, and the flow discharge was small, resulting in the formation of three water nappe. In working condition 4, both the number 1 and number 3 surface holes were opened by 20%, and the water nappes on both sides entered the river channel after collision in the air.
As a result of the different operation models in various working conditions, the range and size of the discharge flow, scouring of the downstream riverbed, and the area of negative pressure on the back surface of the overflow dam were all different.
Different working conditions yielded different throw distances. The longitudinal stretching of the water nappe along the river course was suitable under working conditions 2 and 3, with lengths of 29.3 m and 20.6 m, respectively. Under working condition 4, two water streams did not pass through the notch of the anti-arc segment, and they were collected in the downstream channel after collision in the air without any obvious longitudinal stretching.

It could be seen that when the discharge flow was large, the energy dissipation scheme of a dovetail-shaped slit could cause the water nappe to stretch fully along the river course; the outer edge of the water nappe, however, would be closer to the riverbank slope. Although the water nappe could not be fully stretched along the longitudinal direction under low flow rates, the water nappe entry was located in the main channel, which could meet the flood discharge requirements. In conclusion, this scheme could satisfy the safety flood discharge requirements for the ShiZiYa reservoir.

Author Contributions

Conceptualization, G.L.; Data curation, G.L.; Formal analysis, X.L.; Funding acquisition, G.L.; Investigation, G.L.; Methodology, J.N.; Project administration, G.L.; Resources, G.L.; Software, Y.D.; Validation, X.L.; Visualization, X.L.; Writing—original draft, Y.D.; Writing—review & editing, X.L.

Funding

This research was funded by the Natural Science Foundation of China (Fund No.51579206) and the Shanxi Key Research and Development Program (Fund No.2018SF-352).

Conflicts of Interest

The authors declare no conflict of interest.

References

Zheng, X. Numerical and Experimental Study on the Hydraulic Characteristics of Spillway. Ph.D. Thesis, Sichuan University, Chengdu, China, 2004. (In Chinese). [Google Scholar]
Zhou, X. Computational Hydraulics; Tsinghua University Press: Beijing, China, 1995. (In Chinese) [Google Scholar]
Chen, Y. Experimental Study on the Design of Spillway with High Water Head and Large Unit Discharge. Ph.D Thesis, Xi'an Technology of University, Xi'an, China, 2007. (In Chinese). [Google Scholar]
Lin, J. Hydraulic Structure, 5th ed.; China Water & Power Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
Zhu, Y.; Zhang, F.; Xu, W. Research on hydraulic characteristics of flip bucket with tongue-type. Sci. Technol. Eng. 2004, 4, 397–402. (In Chinese) [Google Scholar]
Deng, J.; Yang, Z.L.; Tian, Z. A new type of leak-floor flip bucket. Sci. China Technol. Sci. 2016, 59, 565–572. [Google Scholar] [CrossRef]
Zhang, M. The research of the atomization and protective measures of the spillway of the Jinping-I Hydropower Station. Des. Hydroelectr. Power Stn. 2015, 31, 24–27. (In Chinese) [Google Scholar]
Mo, H.; Chen, H.; Luo, L. Study on regularity of miter flip bucket's nappe width changing with oblique angle. Water Resour. Power 2013, 13, 124–126. (In Chinese) [Google Scholar]
Zhang, S.; Chen, H.; Zhang, K. The hydraulic calculation research of water tongue pitch of miter flip bucket. China Water Transp. 2008, 8, 160–161. (In Chinese) [Google Scholar]
You, X.; Zeng, Y. The layout and design of flood discharge and energy dissipation for Jinping-I Hydropower Station. The second national collection of papers on the development and application of new materials for the safety and abrasion resistance of hydraulic drainage buildings. In Proceedings of the Second National Seminar of the Development and Application of New Materials for the Safety and Abrasion Resistance of Hydraulic Drainage Buildings, Shenzhen, China, December 2010; pp. 115–119. (In Chinese). [Google Scholar]
Mao, D.; Zhang, F.; Zhong, X.; Lv, M. Application test of swallow-tailed flip bucket ski-jump energy dissipation for Huangdeng hydropower station. Water Resour. Power 2016, 3, 104–107. (In Chinese) [Google Scholar]
Dai, Y.; Qi, X.; Liu, S. The design of dovetail-shaped for Laos South Coconut II hydropower station spillway. Yunnan Water Power 2013, 3, 19–21. (In Chinese) [Google Scholar]
Qiu, Y.; Gong, A.; Dai, X. The experimental study on energy dissipation of Oblique Bucket of the Yunnan TaiHua water reservoir. Pearl River 2015, 36, 22–24. (In Chinese) [Google Scholar]
Wu, X.; Sun, D.; Gao, A. Study on impact from skew bucket on trajectory bucket energy dissipation for flood discharge tunnel. Water Resour. Hydropower Eng. 2014, 45, 56–61. (In Chinese) [Google Scholar]
Patankar, S.V.; Spalding, D.B. Heat and Mass Transfer in Boundary Layers: A General Calculation Procedure; Morgan-Grampian: London, UK, 1967. [Google Scholar]
Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corporation and McGraw Hill Book Company: New York, NY, USA, 1980. [Google Scholar]
Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundary. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
Xia, P. 3-D numerical simulation on the spillway tunnel with Dovetail-shaped flip bucket. China Rural Water Hydropower 2015, 6, 124–128. (In Chinese) [Google Scholar]
Wu, C. Hydraulics; Higher Education Press: Beijing, China, 1983. (In Chinese) [Google Scholar]
Savage, B.M.; Crookston, B.M.; Paxson, G.S. Physical and numerical modeling of large headwater ratios for a 15° labyrinth spillway. J. Hydraul. Eng. 2016, 142, 04016046. [Google Scholar] [CrossRef]

Figure 1. Geometrical configuration of the model flip bucket with dovetail slit (units: cm).

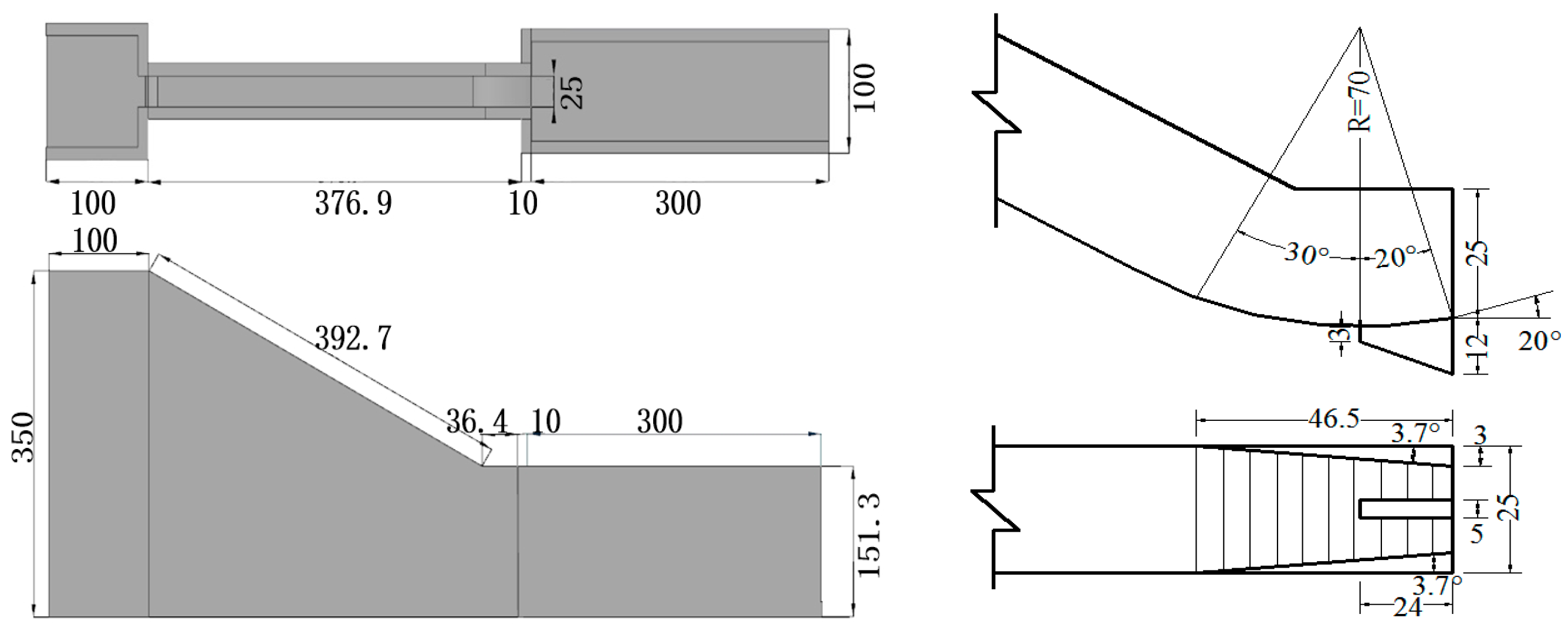
Water 11 00242 g001

Figure 2. General layout of the experiment setup.

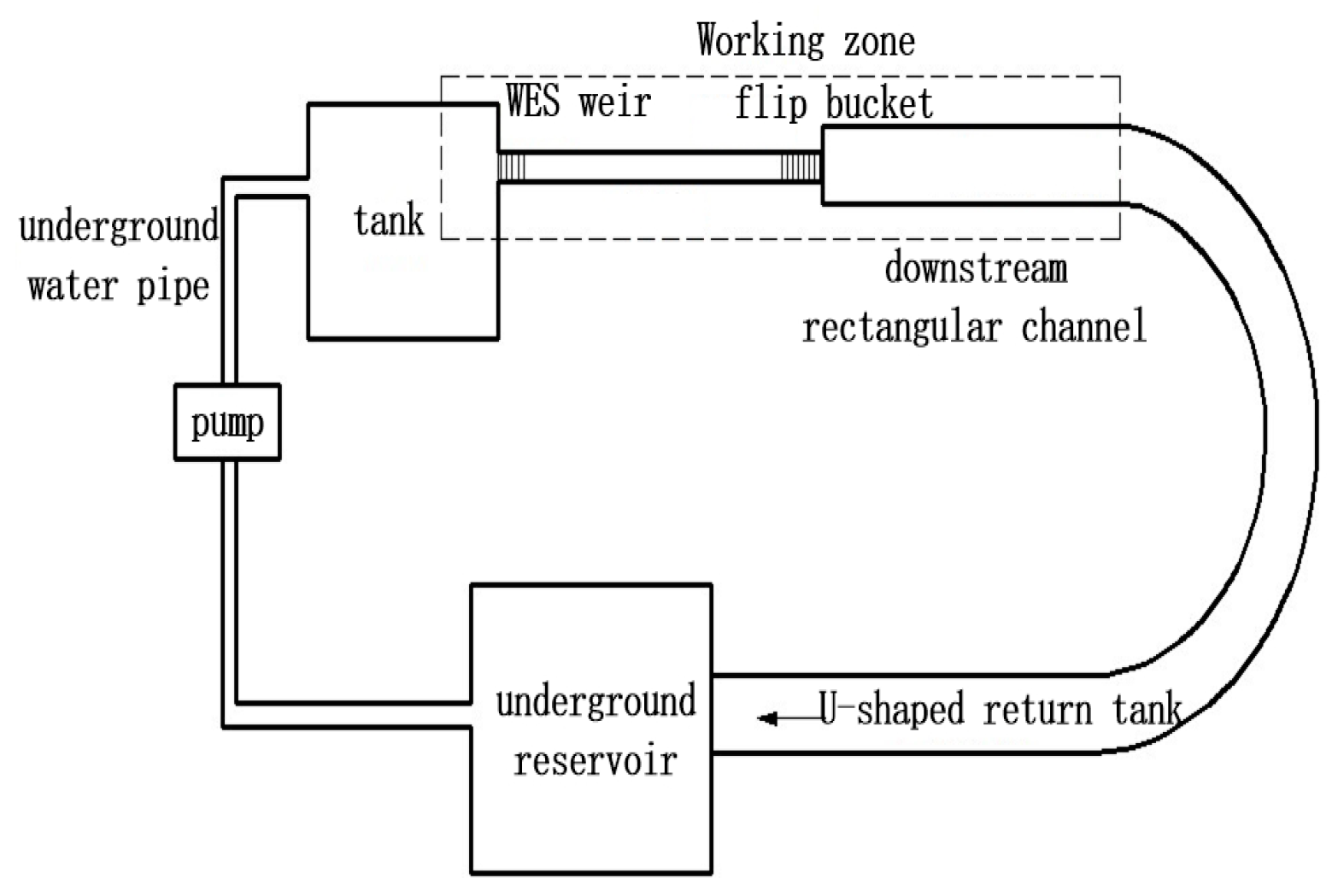
Water 11 00242 g002

Figure 3. Point gauge and sharp-crested weir.

Water 11 00242 g003

Figure 4. Specified boundary conditions for model computation.

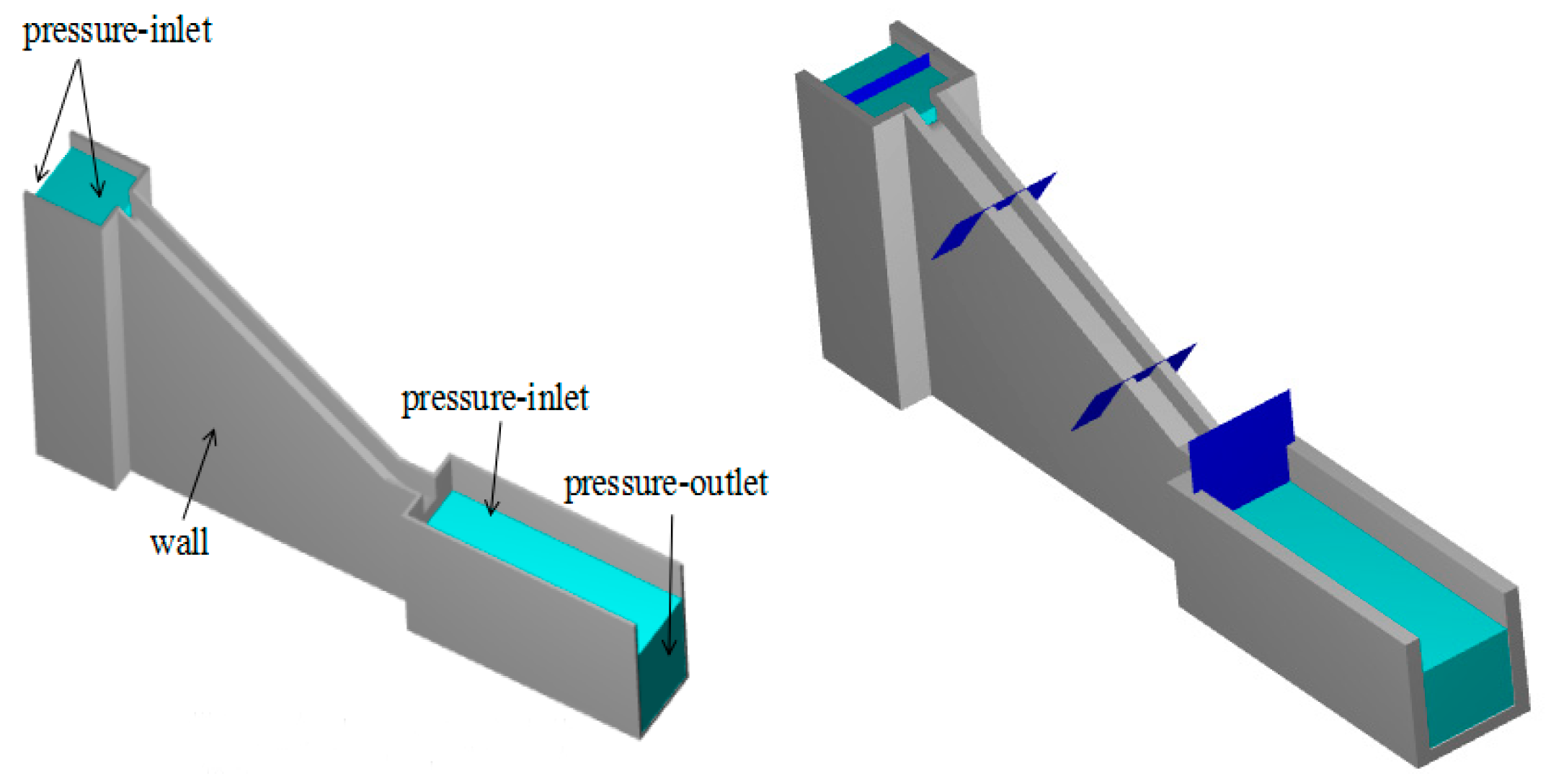
Water 11 00242 g004

Figure 5. Water nappe flow patterns with a swallow-tailed bucket.

Water 11 00242 g005

Figure 6. Comparison of experimental and simulated wall pressures with the swallow-tailed bucket.

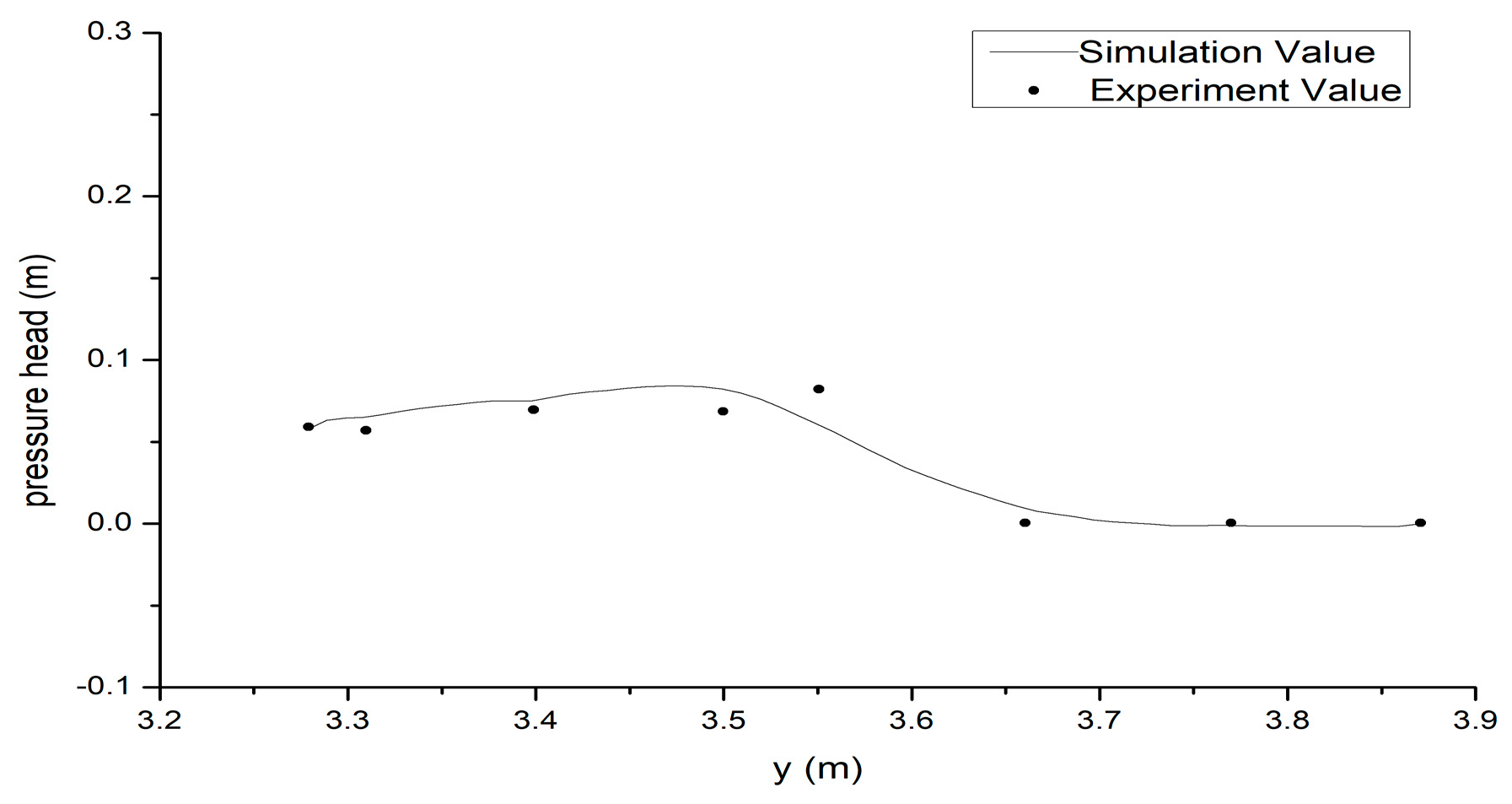
Water 11 00242 g006

Figure 7. Plane view of the overflow dam section (unit: m).

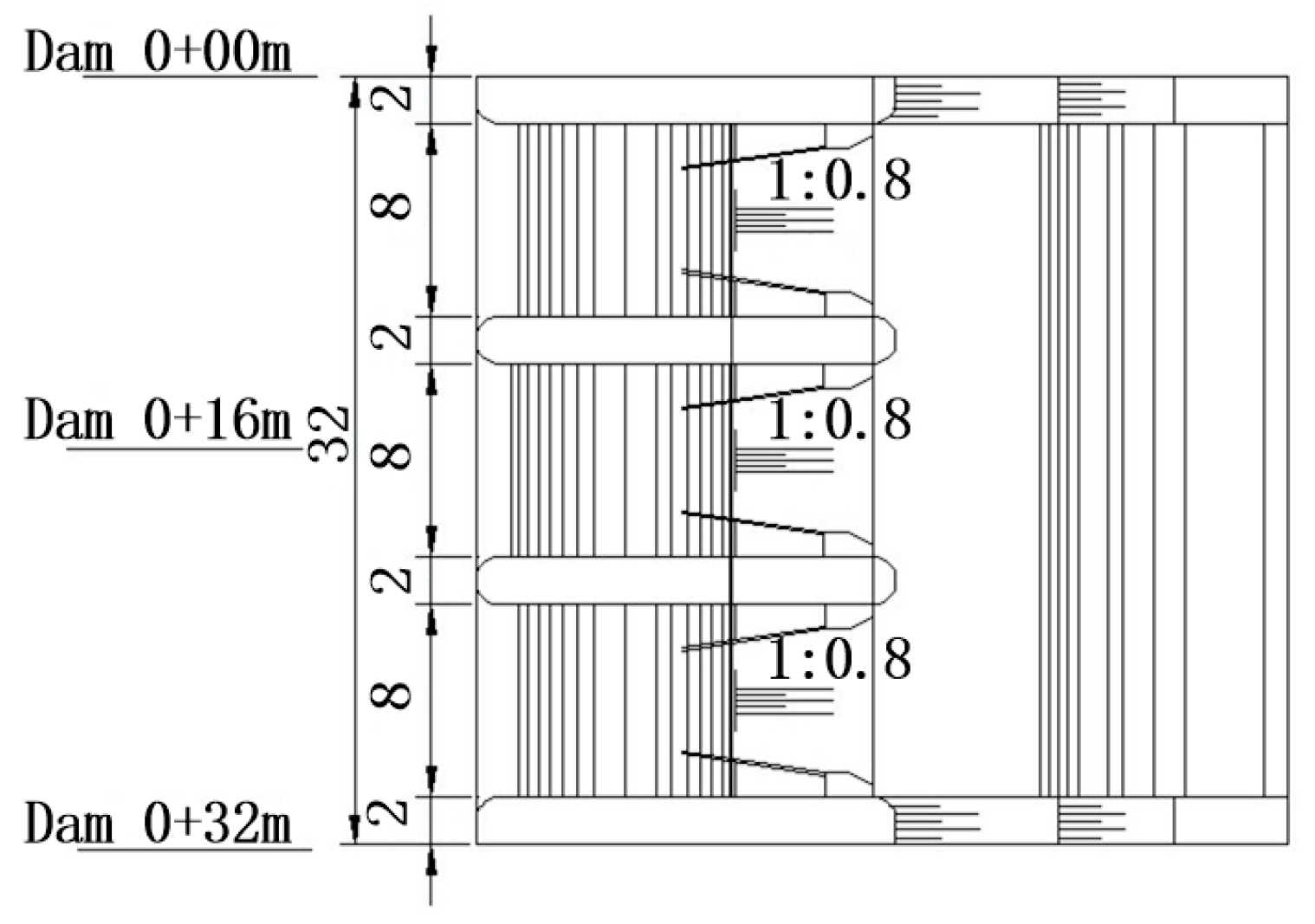
Water 11 00242 g007

Figure 8. Geometrical configuration of the swallow-tailed bucket (unit: m).

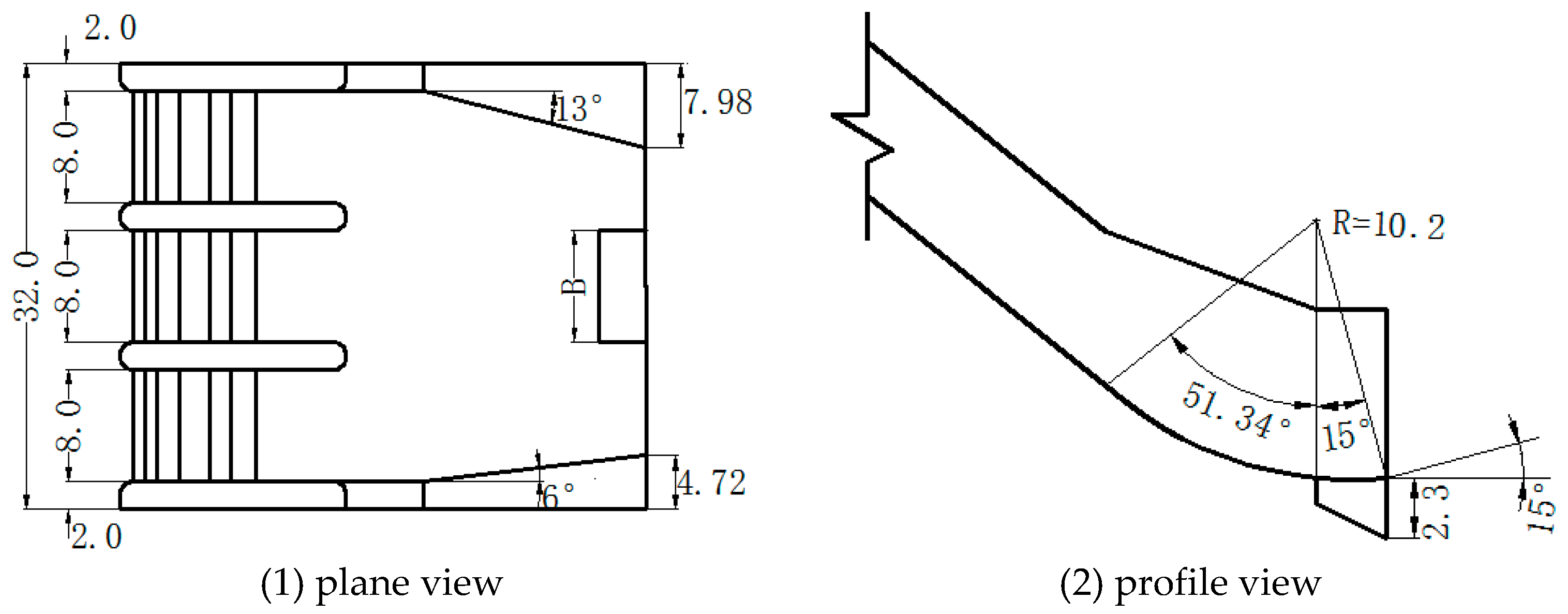
Water 11 00242 g008

Figure 9. Geometrical model of the ShiZiYa reservoir system (design).

Water 11 00242 g009

Figure 10. Specified boundary conditions for ShiZiYa reservoir.

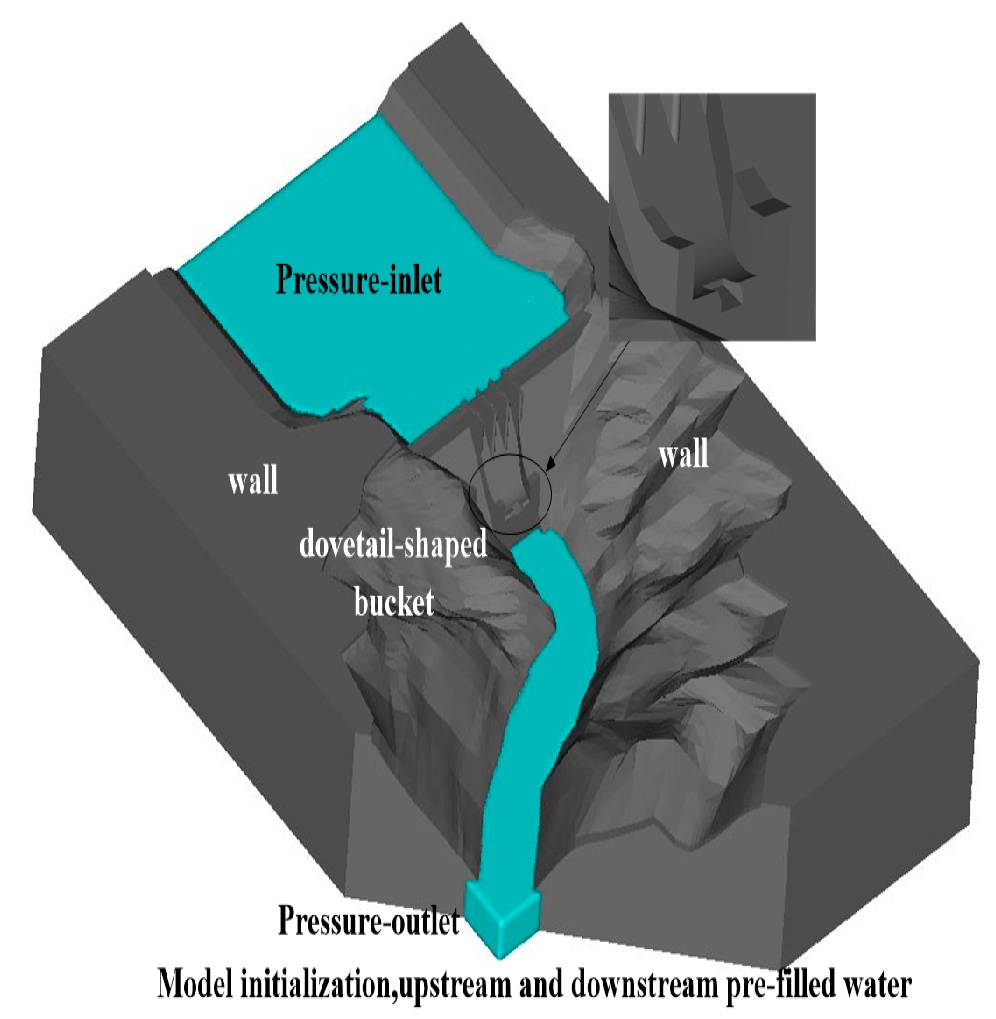
Water 11 00242 g010

Figure 11. Nappe distribution of each scheme under the conditions of a 200-year flood.

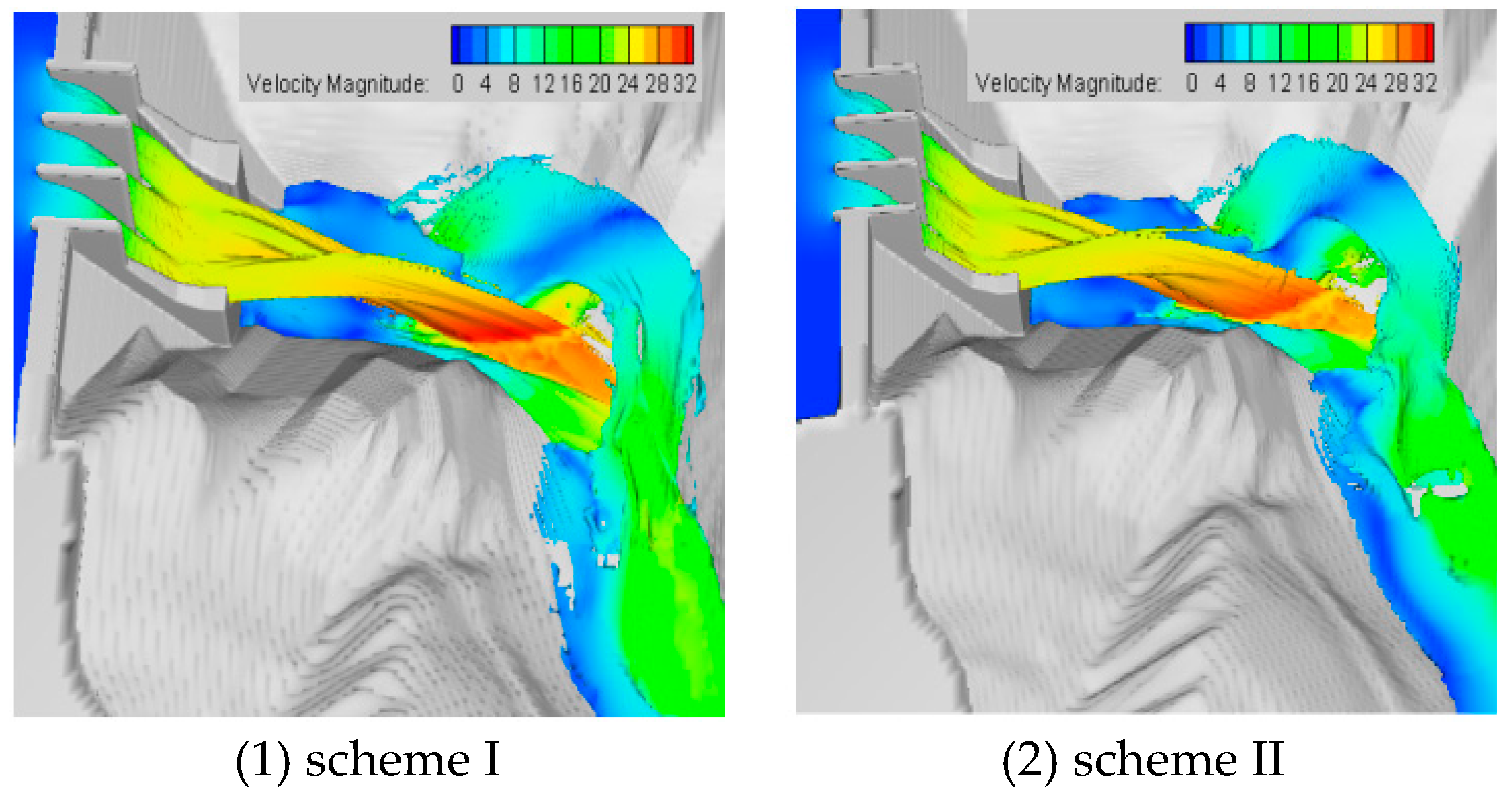
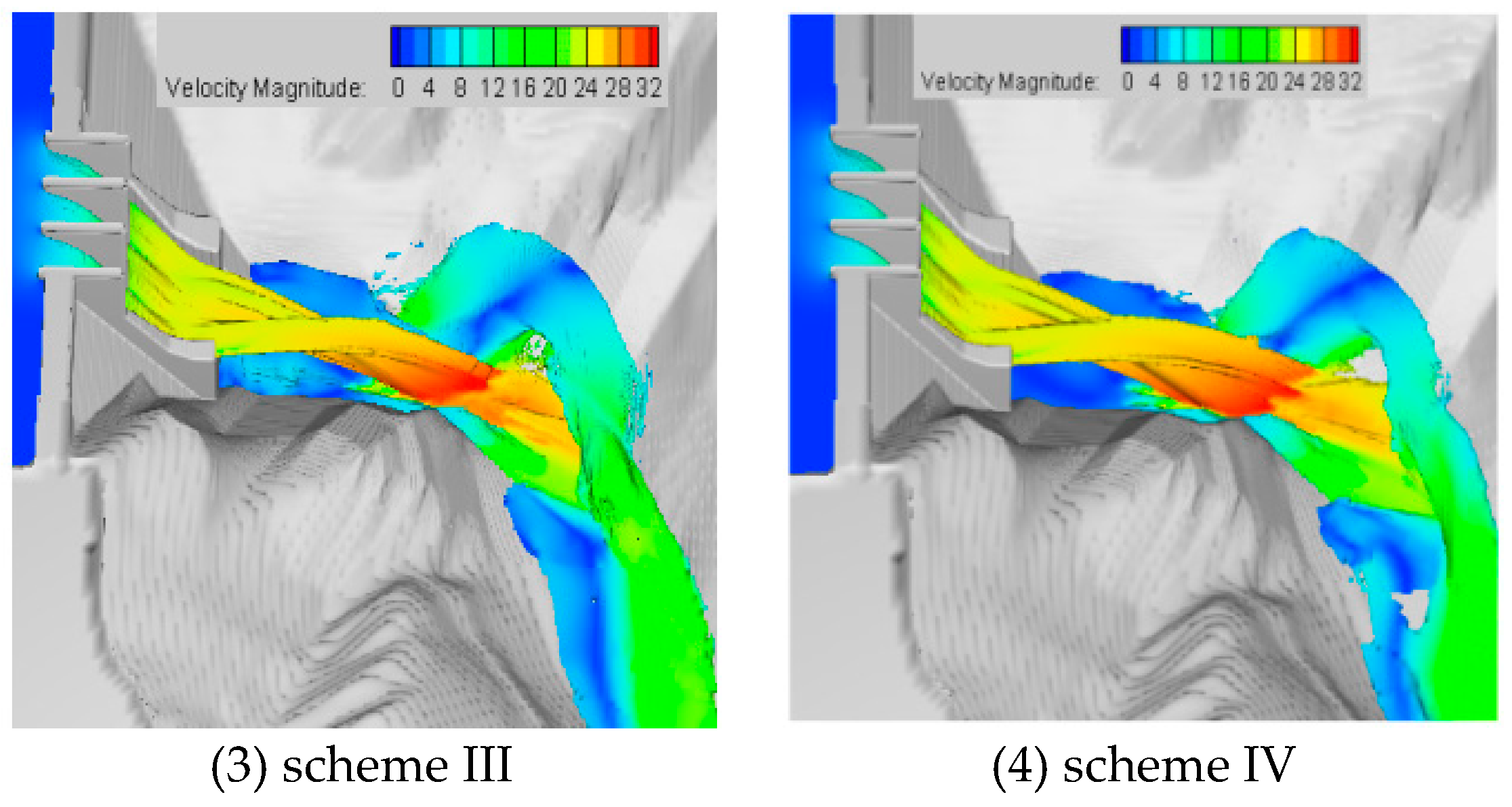
Water 11 00242 g011a Water 11 00242 g011b

Figure 12. Flow patterns and the position of nappe entry into the downstream channel for each working condition.

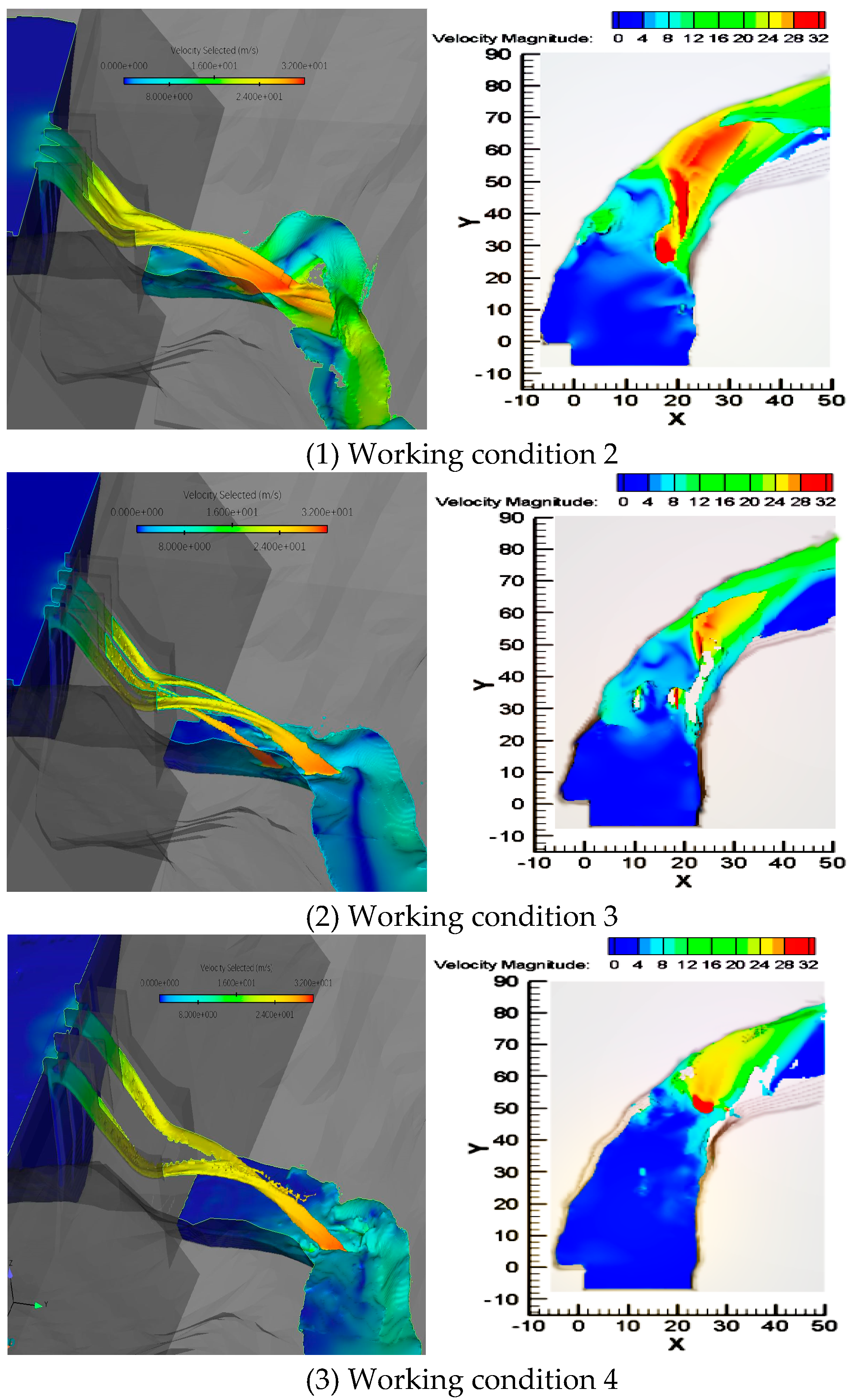
Water 11 00242 g012

Figure 13. Near-bottom flow velocity on the spillway surface and the downstream channel.

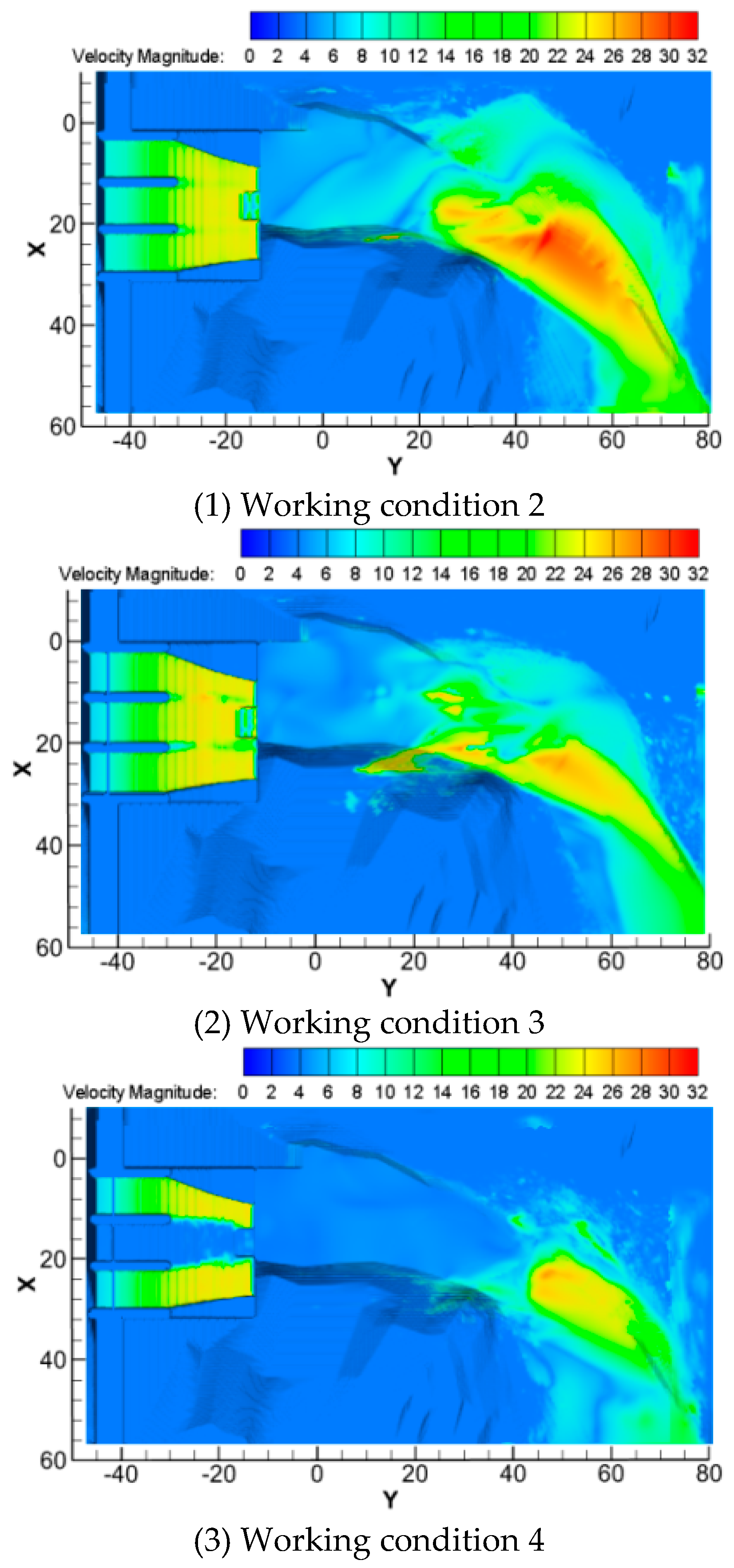
Water 11 00242 g013

Figure 14. Wall surface pressure distribution on the discharge structures.

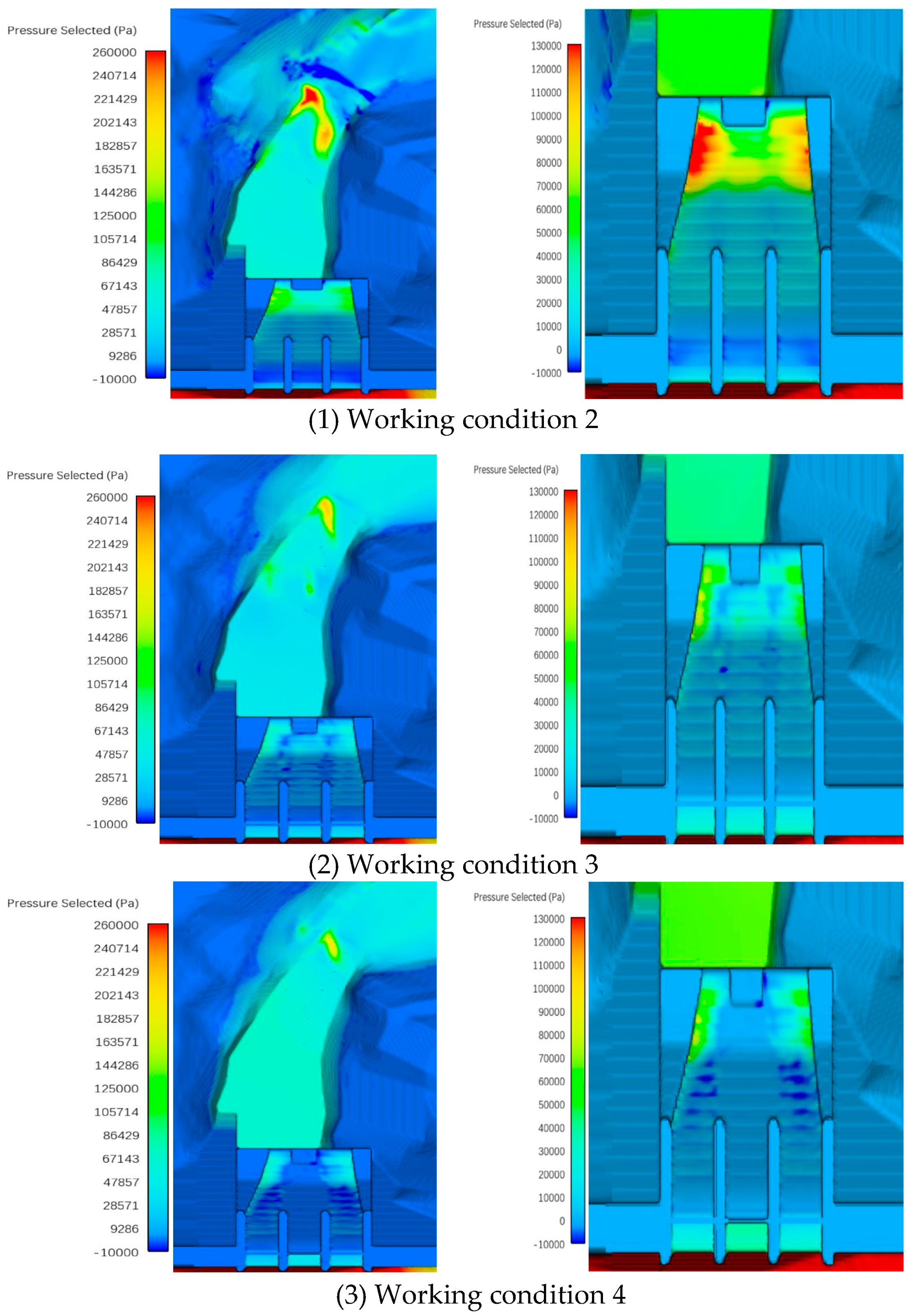
Water 11 00242 g014

Figure 15. Surface pressure distribution on the spillway wall under different working conditions.

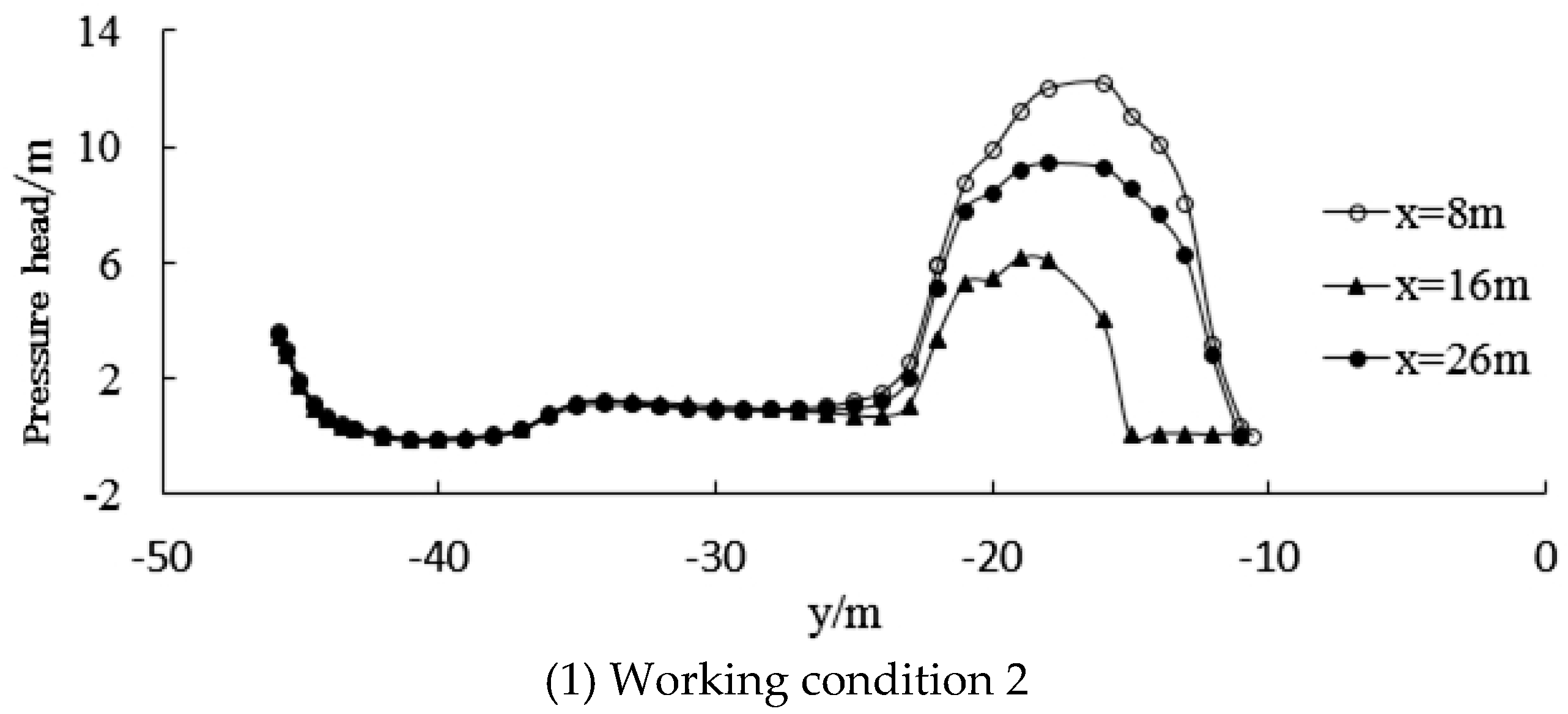
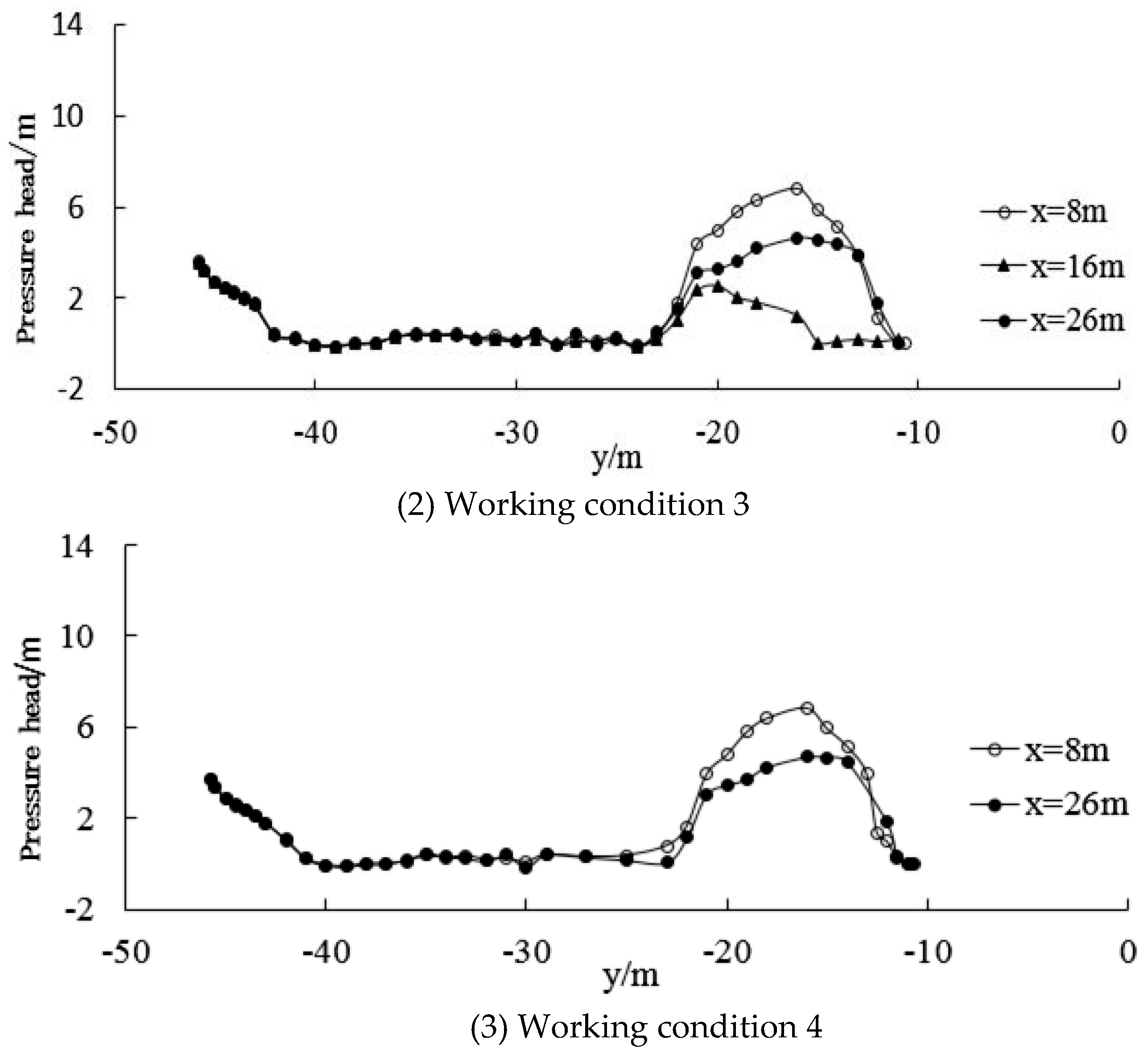
Water 11 00242 g015a Water 11 00242 g015b

Figure 16. Inner and outer edges of the water nappe under different working conditions.

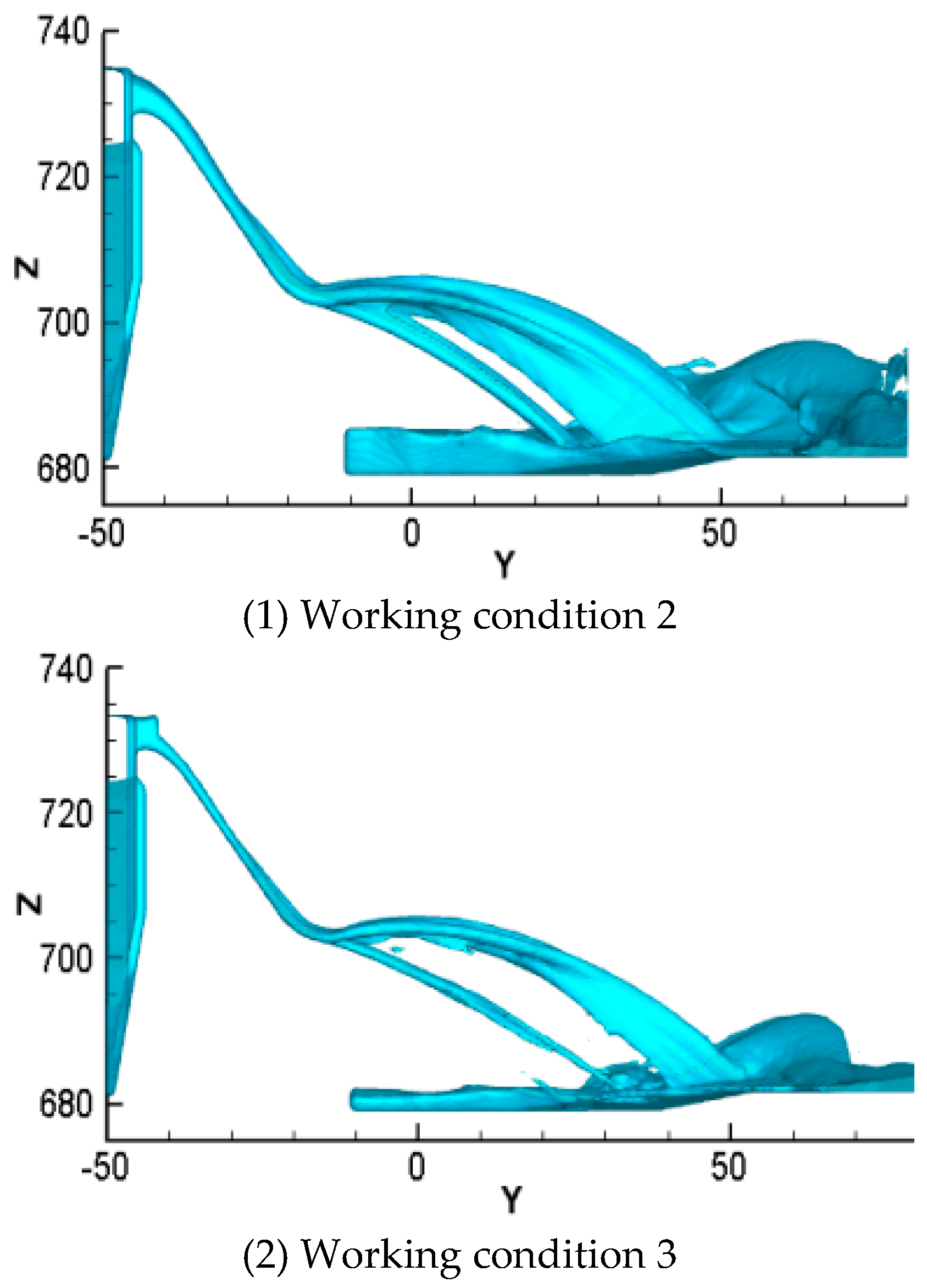
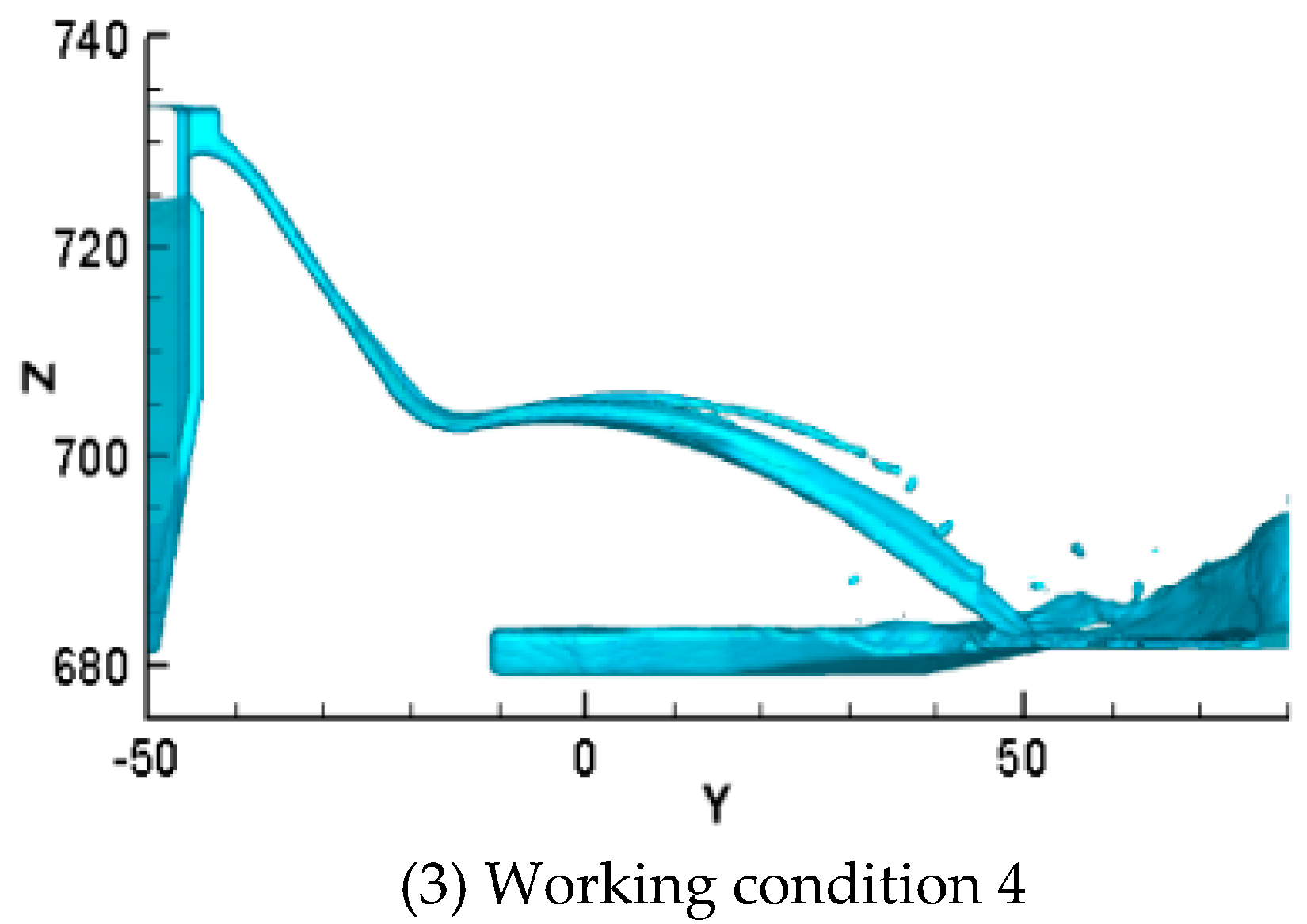
Water 11 00242 g016a Water 11 00242 g016b

Table 1. Working conditions for the calculation.

Modeling Scheme	Working Condition A	Working Condition B	Working Condition C
Flow Rate (m³/s)	0.030	0.025	0.020
Flow Depth (m)	0.143	0.127	0.109

Table 2. GCI calculation results.

Mesh Size D (m)	Total Grid (Millions)	$r (D_{k} / D_{k + 1})$	Q (m³/s)	Fractional Error $\| ε \| = \| \frac{Q_{k} - Q_{k + 1}}{Q_{k + 1}} \|$	$G C I = \frac{F_{s} \| ε \|}{r^{p} - 1} \times 100 (%)$
0.018	5.04	-	2.997808 × 10⁻²	-	-
0.015	7.02	1.2	3.017997 × 10⁻²	0.006895	4.18
0.010	9.37	1.5	3.022485 × 10⁻²	0.001485	0.37

Table 3. Comparison of the experimental and simulation results with a swallow-tailed bucket.

Working Condition	Inner Edge Jet Trajectory Length (m)		Relative Error (%)	Outer Edge Jet Trajectory Length (m)		Relative Error (%)	Water Nappe Highest Point (m)		Relative Error (%)
Working Condition	Experimental Value	Simulation Value	Relative Error (%)	Experimental Value	Simulation Value	Relative Error (%)	Experimental Value	Simulation Value	Relative Error (%)
A	0.37	0.37	0.00	2.17	2.14	1.38	0.52	0.48	7.69
B	0.43	0.41	4.65	1.97	1.93	2.03	0.45	0.42	6.67
C	0.47	0.46	2.13	1.78	1.77	0.56	0.43	0.39	9.30

Table 4. Designed schemes for the swallow-tailed bucket.

Scheme	Left/Right Side-Wall Deflecting Angle	Width of Dovetail-Shaped Bucket (m)	Deflecting Angle of Dovetail Slit
I	θ₁ = 13°, θ₂ = 6°	6	θ₃ = 0°
II	θ₁ = 13°, θ₂ = 6°	6	θ₃ = −5°
III	θ₁ = 13°, θ₂ = 6°	8	θ₃ = 0°
IV	θ₁ = 13°, θ₂ = 6°	8	θ₃ = −5°

Table 5. Characteristics of the water level and discharge conditions used in the numerical simulations.

Working Condition	Flood Standard	Gate Opening (Numerical Simulation)	Maximum Reservoir Water Level (m)	Rated Flow Rate of Flood Discharge Building (m³/s)	Tail Water Level (m)
1	Check flood standard: once in 200 years	Three-hole full opening	735.5	672	689.7
2	Design flood standard: once in 30 years	Three-hole full opening	734.8	506.2	688.6
3	Energy dissipation and anti-impact design standard: once in 20 years	Three-hole opening 20% (e = 1.5 m)	733.4	345.9	687.2
4	Flood standard: once in 5 years	#1, #3 table opening 20% (e = 1.5 m)	733.4	230.6	685.3

Table 6. Analysis of the water nappe features under different working conditions of the swallow-tailed bucket scheme II.

Modeling Scheme	Working Condition 2	Working Condition 3	Working Condition 4
Inner edge jet trajectory length (m)	32.8	41.7	56.4
Outer edge jet trajectory length (m)	62.1	62.3	60.9
Longitudinal stretch length (m)	29.3	20.6	4.5
Water nappe highest point (m)	706.63	705.93	706.4

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

englandsuccart.blogspot.com

Source: https://www.mdpi.com/2073-4441/11/2/242/htm